Why You Should Care About Partial Differential Equations (PDEs)

Aishwarya Balaji

aishbsk

Follow

hugging-science

BryanBradfo

BryanBradfo

Follow

hugging-science

Jose Manuel Nápoles

napoles3d

Follow

hugging-science

Prateik Sinha

Prateik11

Follow

hugging-science

Roey Ben Chaim

roeybc

Follow

hugging-science

Source: Mike Wall in Space

You might recognize this picture of a swirling black hole from Interstellar, the 2014 Christopher Nolan film. What you might not know is that the picture was ultimately made possible by Einstein’s field equations, which are a set of partial differential equations (PDEs) describing how gravity bends light and warps space-time. A known solution to those equations was used to simulate how light would move near a spinning black hole.

PDEs are all around us, from movie animations (like Interstellar), the MRIs and CT scans we get at hospitals (which rely on the Navier-Stokes equations), and even financial markets (the black scholes equation for options pricing). So, what exactly is a PDE?

What are PDEs?

Partial Differential Equations (PDEs) are the mathematical language for modeling systems that depend on multiple independent variables. These variables include spatial coordinates and time, describing how they change and interact across dimensions. They are the equations that explain how physical phenomena behave. They tell us not just if something changes, but how it changes in multiple dimensions simultaneously.

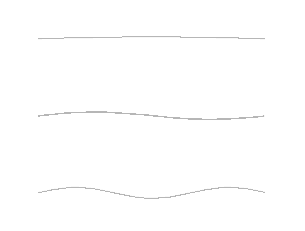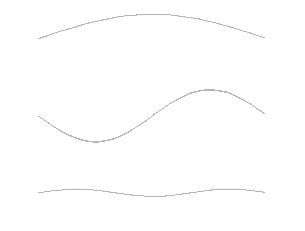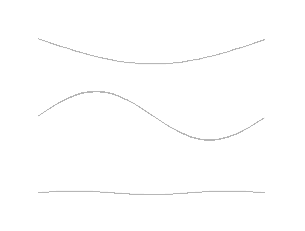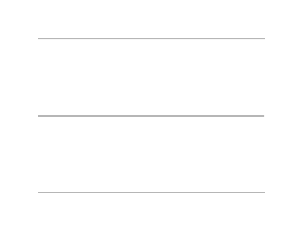
You may have also heard about Ordinary Differential Equations (ODEs). The main difference between an "Ordinary" and a "Partial" one lies in what the system's state depends on.

	ODE	PDE
Definition	Describes a system whose state depends on only one independent variable, usually time.	Describes a system whose state depends on multiple independent variables, like time and one or more spatial dimensions.
Image	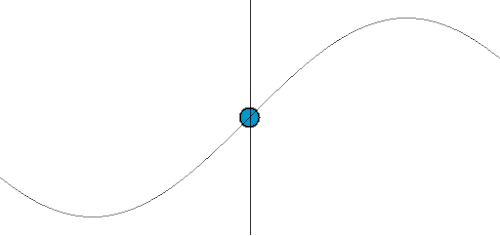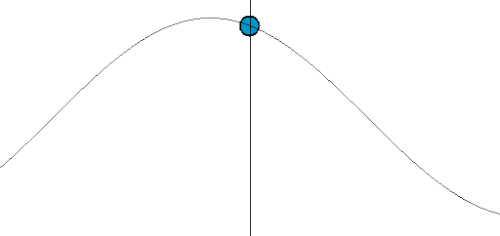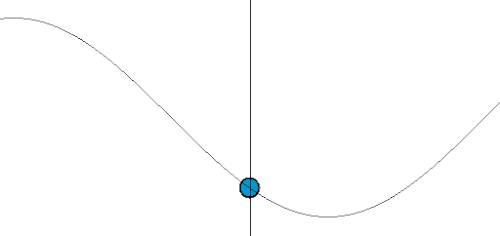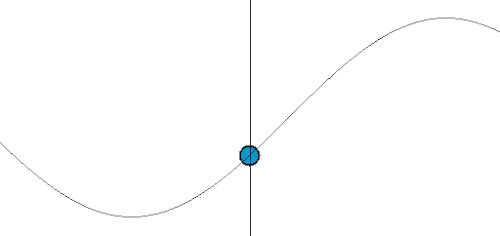Source: Wikipedia	Source: Wikipedia
Example	ODE for a Harmonic Oscillator: The position of the mass, y, changes only as a function of time, t. We write this as y(t). We only need to know when. A simple harmonic oscillator is described by the equation: $$m\frac{d^{2}y}{d{t}^2}=-kym\; \backslash frac\{d^2y\}\{dt^2\}\; =\; -k\; y$$	PDE for a Guitar String: The shape of a vibrating string, u, depends on both the position along the string, x, and the time, t. We write this as u(x, t). We need to know where and when. To describe the string's motion, you need a rule that connects the change in time to the change in space. This is exactly what a PDE does. A famous example is the Wave Equation: $$\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{t}^2}=c^2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}\backslash frac\{\backslash partial^2u\}\{\backslash partial\; t^2\}\; =\; c^2\; \backslash frac\{\backslash partial^2u\}\{\backslash partial\; x^2\}$$

So, to use the cake analogy: an ODE tracks the temperature at one specific point over time, Temperature(time), while a PDE gives you the thermal map of the entire cake across space and time, Temperature(x, y, z, time).

Here are a few of the most famous PDEs: 

• The Heat Equation: Describes how heat spreads out, smoothing sharp temperature differences. It’s all about diffusion and reaching equilibrium.  $$\frac{\mathrm{\partial }u}{\mathrm{\partial }t}=\alpha \frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}\backslash frac\{\backslash partial\; u\}\{\backslash partial\; t\}\; =\; \backslash alpha\; \backslash frac\{\backslash partial^2\; u\}\{\backslash partial\; x^2\}$$

• The Wave Equation: Governs everything that oscillates, from the sound waves of a guitar string to the electromagnetic waves that power your Wi-Fi. $$\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{t}^2}=c^2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}\backslash frac\{\backslash partial^2\; u\}\{\backslash partial\; t^2\}\; =\; c^2\; \backslash frac\{\backslash partial^2\; u\}\{\backslash partial\; x^2\}$$

• The Navier-Stokes equation: Describes the movement in a Newtonian fluid, thus governing the atmospheric dynamics, oceanic currents, or air flow around a wing, but in general any viscous fluid. Solving the existence and smoothness of the solutions is one of the Millenium problems for which the Clay Institute of Mathematics offers a 1 Million prize for a solution or counterexample.

$$\rho (\frac{\mathrm{\partial }\mathbf{u}}{\mathrm{\partial }t}+(\mathbf{u}\cdot \mathrm{\nabla })\mathbf{u})=-\mathrm{\nabla }p+\mu {\mathrm{\nabla }}^2\mathbf{u}+\mathbf{f}\backslash rho\; \backslash left(\; \backslash frac\{\backslash partial\; \backslash mathbf\{u\}\}\{\backslash partial\; t\}\; +\; (\backslash mathbf\{u\}\; \backslash cdot\; \backslash nabla)\backslash mathbf\{u\}\; \backslash right)\; =\; -\backslash nabla\; p\; +\; \backslash mu\; \backslash nabla^2\; \backslash mathbf\{u\}\; +\; \backslash mathbf\{f\}$$

Classical Approaches

Traditional methods of solving PDEs use a known solution at some point(s) together with the derivative to approximate the solution. All such methods discretize the problem in some way. The more fine-grained the discretization, the more accurate the solution. 

Suppose we know that $y=1y\; =\; 1$ when $x=1x\; =\; 1$, and that the derivative of $yy$ with respect to $xx$ is $2x2x$. If we had to approximate the value of $yy$ at $x=2x\; =\; 2$, we could estimate it would follow the slope of the derivative: $y_{x=2}=1+(2-1)\times (2)=3y\_\{x=2\}\; =\; 1\; +\; (2-1)\backslash times(2)\; =\; 3$.  

If the true function we're dealing with is $y(x)=x^{2}y(x)\; =\; x^2$, this isn't a great approximation to $y(2)=4y(2)\; =\; 4$. But we could make it closer by doing it in two smaller steps:

1. $y_{x=1.5}=1+0.5\times 2=2y\_\{x=1.5\}\; =\; 1\; +\; 0.5\; \backslash times\; 2\; =\; 2$
2. $y_{x=2.0}=2+0.5\times 3=3.5y\_\{x=2.0\}\; =\; 2\; +\; 0.5\; \backslash times\; 3\; =\; 3.5$

As we take smaller steps, our approximation gets closer to the true value of 4. This is the Finite Differences method of solving PDEs, specifically Euler's method. In this method, we can get even more accurate predictions by taking the derivatives in cleverer ways, see Runge-Kutta methods.

In our toy example, we tried to find a solution consistent with our initial known value of $y=1$ at $x=1$. Such problems are classified as initial value problems. If we had to find a solution bounded by a set of such known values, it would be boundary value problem.

There are other methods to approximate PDEs that have different trade-offs:

• The Finite Elements method splits our domain into a discrete number of sections, and uses a simple function (such as a linear function) to approximate each part of the domain, creating a piecewise approximation to our solution

• The Finite Volume Method divides the domain into small control volumes and applies the conservation laws (like conservation of mass, momentum, or energy) to each one. Instead of focusing on values at specific points, it ensures that what flows into a volume equals what flows out. This makes it especially useful for fluid dynamics, where fluxes across boundaries matter.

Plenty of such methods exist, each with its own nuances that distinguish it. But more pressing is what they all have in common: they're all slow.

Regardless of the method we use, we end up having to solve a large and sparse system of equations for each discrete node, of which we need as many as possible to ensure an accurate approximation. Each such discrete node depends on the values of its neighboring nodes, making it difficult to process nodes in parallel. Furthermore, these calculations have to be highly precise in order to prevent the propagation of imprecision. And all this gets us a solution to a single initial/boundary value problem. Which means a small change to our initial conditions requires us to do this all over again.

Classical techniques also do not take advantage of parallelization. Neural networks, now ubiquitous, were also considered wildly impractical for decades because we lacked the computing power to properly realize them. They only flourished because they were able to exploit modern computing hardware (GPUs), which is built for massively parallel operations.

Although numerical solvers can somewhat be parallelized, the inherent sequential nature of the underlying algorithm prevents significant parallelization. 

Solving differential equations appears to be an intrinsically serial process due to progressive time-stepping that proves challenging to parallelize.
— Automating Heterogeneous Parallelism in Numerical Differential Equations

On geometric solvers:
“On sequential computers, complexity is not typically a concern for geometric multi-grid methods.
In parallel, however, implementation issues can lead to large complexities, even for algorithms that exhibit adequate parallelism.”

On algebraic solvers:
“Large stencil sizes can lead to large setup times, even if the operator complexity is small, since various components — particularly coarsening and, to some degree, interpolation — require that neighbors of neighbors are visited.
Thus, one might observe superlinear or even quadratic growth in the number of operations when evaluating the coarse grid or the interpolation matrix.”
— A Survey of Parallelization Techniques for Multigrid Solvers

The entire chapter “1.3 Parallel Computation Issues” from the above source is a highly recommended read if you’re interested.

Now that we have a basic understanding of what PDEs are, our goal is twofold: 

1. To convince you why we need a central place to benchmark and compare models, a leaderboard
2. To encourage you to train models to add to it.

If you are curious, stay tuned for our second blog post where we will discuss machine learning approaches (including PINNs and FNOs)!